Name: Экстремум функции двух переменных
Item: Экстремум функции двух переменных
Author: semestr

Главная » » Экстремум функции двух переменных

22:02 Экстремум функции двух переменных
Алгоритм исследования функции двух переменных на экстремум Исследование функции двух переменных на экстремум проводят по следующей схеме. 1. Находят частные производные `dz/dx` и `dz/dy`. 2. Решают систему уравнений: 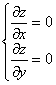и таким образом находят критические точки функции. 3. Находят частные производные второго порядка: 4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀). 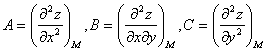5. Делаю вывод о наличии экстремумов: а) если AC – B² > 0 и `A < 0` , то в точке `M` имеется максимум; б) если AC – B² > 0 и `A > 0` , то в точке `M` имеется минимум; в) если AC – B² < 0, то экстремума нет; г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым; Пример решения. z = x^3+xy^2+6xy 1. Найдем частные производные. ${dz}/{dx} = 3 mul x^{2}+y^{2}+6 mul y$ 2. Решим систему уравнений. 3•x²+y²+6•y = 0 2•x•y+6•x = 0 Получим: а) Из первого уравнения выражаем x и подставляем во второе уравнение: б) Из первого уравнения выражаем y и подставляем во второе уравнение: y = -3 3•x²-9 = 0 Количество критических точек равно 4. $M_{1}(0;-6), M_{2}(- sqrt{3};-3), M_{3}(0;0), M_{4}(sqrt{3};-3)$ 3. Найдем частные производные второго порядка. ${d^{2}z}/{dxdy} = 2 mul y+6$ ${d^{2}z}/{dx^{2}} = 6 mul x$ ${d^{2}z}/{dy^{2}} = 2 mul x$ 4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀). Вычисляем значения для точки M₁(0;-6) $A = {{d^{2}z}/{dx^{2}}}_{(0;-6)}$ $C = {{d^{2}z}/{dy^{2}}}_{(0;-6)}$ $B = {{d^{2}z}/{dxdy}}_{(0;-6)}$ AC - B² = -36 < 0, то экстремума нет. Вычисляем значения для точки: $M_{2}(- sqrt{3};-3)$ $A = {{d^{2}z}/{dx^{2}}}_{(- sqrt{3};-3)}$ $C = {{d^{2}z}/{dy^{2}}}_{(- sqrt{3};-3)}$ $B = {{d^{2}z}/{dxdy}}_{(- sqrt{3};-3)}$ $AC - B^{2} = 36 > 0 и A < 0 , то в тorке M_{2}(- sqrt{3};-3) имеется максимум z(- sqrt{3};-3) = 6 sqrt{3}$ Вычисляем значения для точки M₃(0;0) $A = {{d^{2}z}/{dx^{2}}}_{(0;0)}$ $C = {{d^{2}z}/{dy^{2}}}_{(0;0)}$ $B = {{d^{2}z}/{dxdy}}_{(0;0)}$ AC - B² = -36 < 0, то экстремума нет. Вычисляем значения для точки: $M_{4}(sqrt{3};-3)$ $A = {{d^{2}z}/{dx^{2}}}_{(sqrt{3};-3)}$ $C = {{d^{2}z}/{dy^{2}}}_{(sqrt{3};-3)}$ $B = {{d^{2}z}/{dxdy}}_{(sqrt{3};-3)}$ $AC - B^{2} = 36 > 0 и A > 0 , то в тorке M_{4}(sqrt{3};-3) имеется minимум z(sqrt{3};-3) = -6 sqrt{3}$ Вывод*: В точке M₂(-sqrt(3);-3) имеется максимум z(-sqrt(3);-3) = 6 sqrt(3); В точке M₄(sqrt(3);-3) имеется минимум z(sqrt(3);-3) = -6 sqrt(3);
1 2 3 4 5 Просмотров: 1829 \| Добавил: semestr \| Рейтинг: 0.0/0