Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M₀(x₀,y₀,z₀) имеет вид:
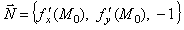
Вектор называется вектором нормали к поверхности σ в точке М₀. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М₀ называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нор ... Читать дальше »